hypothesis - property based testing

quick recap - unit testing

• unit

• written by programmers

• fast

Unit test - Post by Martin Fowler

pytest demo - 01_test_code_add.py

• ill defined tests

• repeated code

This is what frameworks are for

pytest demo - 02_test_code_add_param.py

All tests are passing!

Does it work?

def test_add_numbers_zero_and_one():
    assert add_numbers(0, 121) == 121

def add_numbers(n1, n2):
    if (n2 % 11) == 0 and n1 == 0:
        return n1
    return n1 + n2

What should we be testing?

The addition operator properties

Commutativity

$a + b \equiv b + a$

Associativity

$a + (b + c) \equiv (a + b) + c$

Identity

$a + 0 = a $

# %load 03_test_add_hypothesis.py
from hypothesis import given
from hypothesis import strategies as st

from code_add import add_numbers


@given(st.integers(), st.integers())
def test_code_add_commutativity(a, b):
    assert add_numbers(a, b) == add_numbers(b, a)


@given(st.integers())
def test_code_add_identity(a):
    assert add_numbers(a, 0) == a


@given(st.integers(), st.integers(), st.integers())
def test_code_add_associativity(a, b, c):
    assert add_numbers(
        a,
        add_numbers(b, c)
    ) == add_numbers(
        add_numbers(a, b),
        c
    )

hypothesis

QuickCheck

1 - Assertions are written about logical properties that a function should fulfill
2 - QuickCheck attempts to generate a test case that falsifies such assertions
3 - QuickCheck tries to reduce it to a minimal failing subset by removing or simplifying input data that are unneeded to make the test fail

Property based testing

Hypothesis - what is property based testing?

The thing that QuickCheck does

Fuzzy testing

Input

• Random
• Malformed
• Invalid

Output

• Crash
• Exceptions
• Assertions
• Memory leaks

End user POV

• A fuzzer
• A library of tools for making it easy to construct property-based tests using that fuzzer

Dissecting our example

from hypothesis import strategies as st

Most things should be easy to generate and everything should be possible.

Hypothesis - what can you generate?

help(st.integers)

Help on function integers in module hypothesis.strategies._internal.core:

integers(min_value=None, max_value=None)
    Returns a strategy which generates integers; in Python 2 these may be
    ints or longs.
    
    If min_value is not None then all values will be >= min_value. If
    max_value is not None then all values will be <= max_value
    
    Examples from this strategy will shrink towards zero, and negative values
    will also shrink towards positive (i.e. -n may be replaced by +n).

from hypothesis import given

help(given)

Help on function given in module hypothesis.core:

given(*_given_arguments, **_given_kwargs)
    A decorator for turning a test function that accepts arguments into a
    randomized test.
    
    This is the main entry point to Hypothesis.

the good stuff

• pytest integration
• strategies for most common types
• composite strategy to generate new strategies
• compositional shrinking of examples
  • Integrated shrinking on hypothesis
  • Compositional Shrinking on hypothesis
• a database of failing examples to check regressions
  • read this Anatomy of a Hypothesis Based Test
• Hypothesis for the Scientific Stack: pandas/numpy strategies

Some cool examples*

* The opinions expressed on this slide are my own and not necessarily those of my employers

Sorting

• sort(l) returns a list
• sorted list has the same elements
• there is an ordering between elements
• sorting a sorted list does not change anything

The more things change, the more they stay the same

Let's see how that looks

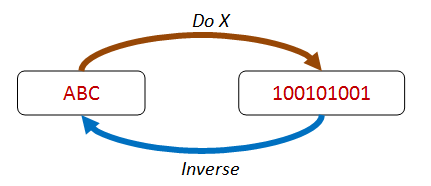
There and back again

An example with a binary encoder/decoder

import pytest

examples = [("1", 1), ("0", 0), ("10", 2), ("11", 3), ("100", 4)]

@pytest.mark.parametrize("b,i", examples)
def test_examples(b, i):
    assert from_binary(b) == i
    assert to_binary(i) == b

def to_binary(i):
    res = []
    while i != 0:
        i, mod = divmod(i, 2)
        res.append(mod)
    if len(res) == 0:
        res.append(0)
    return "".join(map(str, res))[::-1]

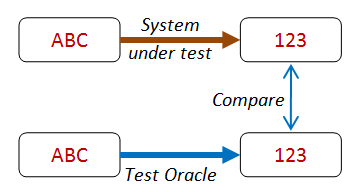
Test oracle

The change making problem

Let $S = \{w_1, w_2, \ldots, w_n \mid w_i < w_j \forall i < j, w_i \in \mathbb{Z}^+ \}$ a coin system ($1$ should always be present)

Let $W \in \mathbb{Z}^+$.

Let $x_i$ be the amount of coins of denomination $w_i$

$ \begin{equation*} \begin{aligned} & \text{minimize} & & \sum_{j=0}^{n}(x_j) \\ & \text{subject to} & & \sum_{j=0}^{n} w_j x_j = W \end{aligned} \end{equation*} $

And let $S$ be tagged as canonical if $G_r(W,S) = D_p(W,S) \forall W$ where $G_r$ is the solution provided by the greedy algorithm and $D_p$ the dynamic programming solution.

How can we find a non-canonical system?

Let hypothesis find one for us

A note on verbosity

What examples is hypothesis running?

We can see an example with a prime numbers generator

Cool readings & resources

Choosing properties for property-based testing